الذكاء الاصطناعي الأكثر ذكاءً للرياضيات الحقيقية

إذا كنت تتابع مجال الذكاء الاصطناعي مؤخرًا، فمن المحتمل أنك لاحظت شيئًا كبيرًا: لم يعد الناس يهتمون فقط بما يجيب عليه الذكاء الاصطناعي، بل يهتمون بكيفية وصوله إلى تلك الإجابة. وهذا هو بالضبط ما يتدخل فيه DeepSeek Math V2. إنه نموذج مفتوح المصدر مصمم خصيصًا للاستدلال الرياضي الحقيقي.

في هذا الدليل، سأطلعك على ماهية DeepSeek Math V2، ولماذا يتحدث الجميع عن نظام التحقق من المولدات، وكيف يتمكن هذا النموذج من حل البراهين المعقدة أثناء التحقق من عمله مثل مدرس رياضيات صارم. إذا كان لديك فضول بشأن كيفية تحسن الذكاء الاصطناعي أخيرًا في الرياضيات الرسمية، فاستمر في القراءة.

ما هو DeepSeek Math V2؟

DeepSeek Math V2 هو أحدث برنامج LLM مفتوح المصدر من DeepSeek-AI مصمم خصيصًا للاستدلال الرياضي وإثبات النظريات. تم إطلاقه في نهاية عام 2025، وهو يمثل تحولًا كبيرًا من نماذج الذكاء الاصطناعي التي تعيد ببساطة الإجابات النهائية إلى تلك التي تظهر عملها فعليًا وتبرر كل خطوة.

ما يجعلها مميزة هو إعداد أداة التحقق من المولد ذي النموذجين. يقوم أحد النماذج بكتابة الدليل، بينما يقوم النموذج الثاني بفحص كل خطوة مثل المفتش المنطقي. لذا، بدلًا من مجرد حل مشكلة ما، يقوم DeepSeek Math V2 أيضًا بتقييم ما إذا كان المنطق الخاص به منطقيًا أم لا. وقد قام الفريق بتدريبه من خلال التعلم المعزز، ولم يقتصر الأمر على مكافأة الإجابات الصحيحة فحسب، بل أيضًا على الاشتقاقات الواضحة والدقيقة.

والنتائج تتحدث عن نفسها. يقدم DeepSeek Math V2 أعلى مستوى في مسابقات الرياضيات الكبرى، حيث سجل حوالي 83.3% في IMO 2025 و98.3% في Putnam 2024. وهو يتفوق على النماذج المفتوحة السابقة ويقترب بشكل مدهش من أفضل الأنظمة الخاصة المتوفرة.

الميزات الرئيسية لبرنامج DeepSeek Math V2

• نطاق هائل: من خلال معلمات 685B المبنية على DeepSeek-V3.2-ExpBase، يتعامل النموذج مع البراهين الطويلة للغاية باستخدام تنسيقات رقمية متعددة (BF16، F8_E4M3، F32) والاهتمام المتناثر لإجراء عمليات حسابية فعالة.
• التحقق الذاتي: يقوم مدقق مخصص بفحص كل خطوة إثبات للتأكد من الاتساق المنطقي. إذا كانت إحدى الخطوات خاطئة أو تم تطبيق النظرية بشكل خاطئ، يقوم النظام بوضع علامة عليها ويتم إعادة تدريب المولد لتجنب تكرار الخطأ. تجبر حلقة ردود الفعل هذه النموذج على تحسين منطقه.
• تدريب التعزيز: تم تدريب النموذج على الأدبيات الرياضية والمسائل التركيبية، ثم تم تحسينه من خلال التعلم المعزز القائم على البرهان. يقترح المولد الحلول، ويسجلها المدقق، وتنتج البراهين الأكثر صعوبة مكافآت أقوى، مما يدفع النموذج نحو اشتقاقات أعمق وأكثر دقة.
• مفتوح المصدر ويمكن الوصول إليه: تم إصدار الأوزان ضمن Apache 2.0 وهي متاحة على Hugging Face وGitHub. يمكنك أيضًا تجربة DeepSeek Math V2 مباشرة من خلال واجهة DeepSeek Chat المجانية، والتي تدعم الأبحاث غير التجارية والاستخدام التعليمي.

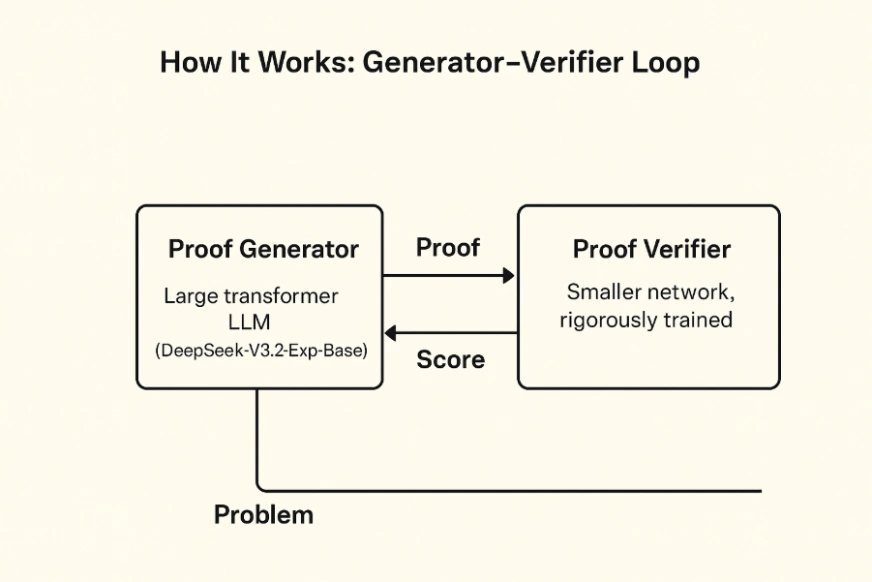
الهندسة المعمارية ذات النموذجين لبرنامج DeepSeek Math V2

تقدم بنية DeepSeek Math V2 مكونين رئيسيين يتفاعلان مع بعضهما البعض:

• مولد الإثبات: يعد هذا المحول الكبير LLM (DeepSeek-V3.2-Exp-Base) مسؤولاً عن إنشاء براهين رياضية خطوة بخطوة بناءً على بيان المشكلة.

• مدقق الإثبات: على الرغم من أنها شبكة أصغر، إلا أنها شبكة مدربة على نطاق واسع وتمثل كل برهان بخطوات منطقية (على سبيل المثال، عبر شجرة تركيب مجردة) وتنفذ تطبيق القواعد الرياضية عليها. فهو يشير إلى التناقضات في الاستدلال أو التلاعبات غير الصالحة التي لا يطلق عليها “كلمات” ويخصص “درجة” لكل دليل.

التدريب يحدث على مرحلتين. أولاً، يتم تدريب المدقق على البراهين المعروفة الصحيحة وغير الصحيحة. ثم يتم تدريب المولد بحيث يكون المدقق بمثابة نموذج المكافأة الخاص به. في كل مرة يقدم المولد دليلا، يقوم المدقق بتسجيله. تتم معاقبة الخطوات الخاطئة، ويتم مكافأة البراهين الصحيحة تمامًا، وبمرور الوقت يتعلم المولد إنتاج اشتقاقات نظيفة وصالحة.

التحقق من المرور المتعدد والبحث

مع تحسن المولد والبدء في إنتاج براهين أكثر صعوبة، يتلقى المدقق حوسبة إضافية مثل تصاريح بحث إضافية لاكتشاف الأخطاء الدقيقة. يؤدي هذا إلى إنشاء هدف متحرك حيث يظل المدقق دائمًا في المقدمة قليلاً، مما يدفع المولد إلى التحسين المستمر.

أثناء التشغيل العادي، يستخدم النموذج أيضًا عملية استدلال متعددة التمريرات. يقوم بإنشاء العديد من مسودات إثبات المرشح، ويقوم المدقق بفحص كل واحدة منها. يمكن لـ DeepSeek Math V2 أن يتفرع إلى بحث بأسلوب MCTS حيث يستكشف مسارات إثبات مختلفة، ويزيل المسارات ذات درجات التحقق المنخفضة، ويكرر المسارات الواعدة. بعبارات بسيطة، يستمر في إعادة كتابة عمله حتى يوافق عليه المدقق.

def generate_verified_proof(problem):
    root = initialize_state(problem)
    while not root.is_complete():
        children = expand(root, generator)
        for child in children:
            score = verifier.evaluate(child.proof_step)
            if score < THRESHOLD:
                prune(child)
        root = select_best(children)
    return root.full_proof

يضمن DeepSeek Math V2 أن كل إجابة تأتي مع تفكير واضح خطوة بخطوة، وذلك بفضل مزيجها من التوليد والتحقق في الوقت الحقيقي. تعد هذه ترقية كبيرة من النماذج التي تهدف فقط إلى الإجابة النهائية دون توضيح كيفية وصولها إليها.

كيفية الوصول إلى DeepSeek Math 2؟

تتوفر أوزان النموذج والكود بشكل عام بموجب ترخيص Apache 2.0 (يذكر DeepSeek بالإضافة إلى ذلك ترخيصًا غير تجاري مناسب للبحث). لتجربتها، يمكنك:

• للتحميل من الوجه المعانق: تتم استضافة النموذج على Hugging Face Deepseek-ai/DeepSeekMath-V2. باستخدام مكتبة Hugging Face Transformers، يمكن للمرء تحميل النموذج والرمز المميز. ضع في اعتبارك أنه ضخم، وستحتاج على الأقل إلى العديد من وحدات معالجة الرسومات المتطورة (يوصي الريبو بـ 8 × A100) أو وحدات TPU للاستدلال.

• واجهة الدردشة DeepSeek: إذا لم يكن لديك حوسبة ضخمة، فإن DeepSeek يقدم عرضًا توضيحيًا مجانيًا على الويب على chat.deepseek.com. تتيح “الدردشة مع DeepSeek AI” هذه المطالبة التفاعلية (بما في ذلك الاستعلامات الرياضية) بدون إعداد. إنها طريقة سهلة لرؤية مخرجات النموذج في مسائل العينة.

• واجهات برمجة التطبيقات والتكامل: يمكنك نشر النموذج عبر أي إطار عمل قياسي للخدمة (على سبيل المثال، يحتوي GitHub الخاص بـ DeepSeek على رمز للاستدلال متعدد التمريرات). يمكن لأدوات مثل Apidog أو FastAPI أن تساعد في تغليف النموذج في واجهة برمجة التطبيقات. على سبيل المثال، يمكن للمرء إنشاء نقطة نهاية /solve-proof تأخذ نص المشكلة وترجع تعليقات النموذج وتعليقات التحقق.

الآن، دعونا نجرب النموذج!

المهمة 1: إنشاء دليل خطوة بخطوة

المتطلبات الأساسية:

1. وحدة معالجة رسومات (GPU) مزودة بذاكرة VRAM سعة 40 جيجابايت على الأقل (على سبيل المثال، A100 أو H100 أو ما شابه ذلك).
2. بيئة بايثون (بايثون 3.10+)
3. تثبيت أحدث الإصدارات من:

pip install transformers accelerate bitsandbytes torch –upgrade 

الخطوة 1: اختر مشكلة الرياضيات

في هذا التدريب العملي، سنستخدم المشكلة التالية وهي شائعة جدًا في أولمبياد الرياضيات:

اجعل a، b، c أرقامًا حقيقية موجبة بحيث يكون a + b + c = 1. أثبت أن a² + b² + c² ≥ 1/3.

الخطوة 2: برنامج بايثون النصي لتشغيل النموذج

from transformers import AutoTokenizer, AutoModelForCausalLM
import torch

# Load model and tokenizer
model_id = "deepseek-ai/DeepSeek-Math-V2"
tokenizer = AutoTokenizer.from_pretrained(model_id, trust_remote_code=True)
model = AutoModelForCausalLM.from_pretrained(
    model_id,
    torch_dtype=torch.bfloat16,
    device_map="auto",
    trust_remote_code=True
)

# Prompt
prompt = """You are DeepSeek-Math-V2, a competition-level mathematical reasoning model.
Solve the following problem step by step. Provide a complete and rigorous proof.
Problem: Let a, b, c be positive real numbers such that a + b + c = 1. Prove that a² + b² + c² ≥ 1/3.
Solution:"""

# Tokenize and generate
inputs = tokenizer(prompt, return_tensors="pt").to(model.device)
outputs = model.generate(
    **inputs,
    max_new_tokens=512,
    temperature=0.2,
    top_p=0.95,
    do_sample=True
)

# Decode and print result
output_text = tokenizer.decode(outputs(0), skip_special_tokens=True)
print("\n=== Proof Output ===\n")
print(output_text)

# Step 3: Run the script
# In your terminal, run the following command:
# python deepseek_math_demo.py

أو إذا كنت تحتاج إلى ذلك، يمكنك اختباره على واجهة الويب أيضًا.

الإخراج:

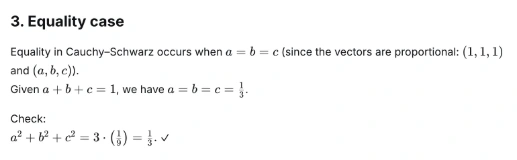
المهمة 2: التحقق من صحة الدليل الرياضي

في هذه المهمة، سنقوم بإطعام DeepSeek Math V2 برهانًا رياضيًا معيبًا ونطلب منه ذلك المدقق عنصر للنقد والتحقق من صحة المنطق. سيُظهر بشكل أساسي إحدى أهم ميزات DeepSeek Math V2، وهي التحقق الذاتي.

الخطوة الأولى: تحديد المشكلة:

الخطوة 2: أضف رمز المطالبة للتحقق:

from transformers import AutoTokenizer, AutoModelForCausalLM
import torch

model_id = "deepseek-ai/DeepSeek-Math-V2"
tokenizer = AutoTokenizer.from_pretrained(model_id, trust_remote_code=True)
model = AutoModelForCausalLM.from_pretrained(
    model_id,
    torch_dtype=torch.bfloat16,
    device_map="auto",
    trust_remote_code=True
)

# Incorrect proof for DeepSeek to verify
incorrect_proof = """
Claim: For all real numbers x, x^2 + 2x + 5 ≥ 0.
Proof: Since x^2 is always positive and 2x + 5 is always positive, their sum is always positive. Hence x^2 + 2x + 5 ≥ 0 for all real x.
"""

prompt = f"""You are the DeepSeek Math V2 Verifier.
Your task is to critically analyze the following proof, identify incorrect reasoning,
and provide a corrected, rigorous explanation.
Proof to verify:
{incorrect_proof}
Please provide:
1. Whether the proof is correct or incorrect.
2. Which steps contain mistakes.
3. A corrected proof.
"""

inputs = tokenizer(prompt, return_tensors="pt").to(model.device)
outputs = model.generate(
    **inputs,
    max_new_tokens=600,
    temperature=0.2,
    top_p=0.95,
    do_sample=True
)

print("\n=== Verifier Output ===\n")
print(tokenizer.decode(outputs(0), skip_special_tokens=True))

# Step 3: Run the script
# In your terminal, run the following command:
# python deepseek_verifier_demo.py 

الإخراج:

الأداء والمعايير

يقدم DeepSeek Math V2 نتائج متميزة عبر معايير الرياضيات الرئيسية:

• أولمبياد الرياضيات الدولي (IMO) 2025: حصلت على حوالي 83.3 بالمائة من خلال حل المشكلات من 1 إلى 5 بشكل كامل وحل المشكلة 6 جزئيًا. وهذا يطابق أفضل الأنظمة مغلقة المصدر، حتى قبل دخولها في المسابقة الرسمية.
• أولمبياد الرياضيات الكندي (CMO) 2024: حصل على حوالي 73.8 بالمائة عن طريق حل 4 مشاكل من أصل 6 بشكل كامل وحل الباقي بشكل جزئي.
• امتحان بوتنام 2024: تم تحقيق 98.3 بالمائة (118 من أصل 120 نقطة) في ظل الحوسبة المتدرجة، ولم ينقص سوى رصيد جزئي في أصعب الأسئلة.
• بروف بنش (ديب مايند): حصل على موافقة بنسبة 99 بالمائة تقريبًا على البراهين الأساسية و62 بالمائة على البراهين المتقدمة، متفوقًا على GPT-4، وClaude 4، وGemini في الاستدلال المنظم.

في المقارنات جنبًا إلى جنب، يتفوق DeepSeek Math V2 باستمرار على النماذج الرائدة في دقة الإثبات بنسبة 15 إلى 20 بالمائة. لا تزال العديد من النماذج تخمن الخطوات أو تتخطىها، بينما تعمل حلقة التحقق الصارمة الخاصة بـ DeepSeek على تقليل معدلات الخطأ بشكل كبير، حيث تظهر التقارير أخطاء استدلالية أقل بنسبة تصل إلى 40 بالمائة مقارنة بالأنظمة التي تركز على السرعة.

التطبيقات والأهمية

DeepSeek Math V2 ليس قويا فقط في المسابقات. إنه يدفع الذكاء الاصطناعي إلى الاقتراب من التحقق الرسمي من خلال التعامل مع كل مشكلة على أنها مهمة تدقيق. فيما يلي الطرق الرئيسية التي يمكن استخدامها:

• التعليم والدروس الخصوصية: يمكنه تقييم واجبات الرياضيات والتحقق من إثباتات الطلاب وتقديم تلميحات خطوة بخطوة أو حل المشكلات التدريبية.
• المساعدة البحثية: مفيد لاستكشاف الأفكار المبكرة، واكتشاف المنطق الضعيف، وتوليد أساليب جديدة في مجالات مثل التشفير ونظرية الأعداد.
• أنظمة إثبات النظرية: يمكن أن يدعم أدوات مثل Lean أو Coq من خلال المساعدة في ترجمة منطق اللغة الطبيعية إلى أدلة رسمية.
• ضبط الجودة: يمكنه التحقق من الحسابات المعقدة في مجالات مثل الفضاء الجوي والتشفير وتصميم الخوارزميات حيث تكون الدقة أمرًا بالغ الأهمية.

إقرأ أيضاً:

خاتمة

يعد DeepSeek Math V2 أداة قوية بين المهام المتعلقة بالرياضيات في الذكاء الاصطناعي. فهو يربط العمود الفقري للمحولات الضخمة بحلقات جديدة لفحص الإثبات، ويحقق درجات قياسية في المسابقات، ويتم إتاحته للمجتمع مجانًا. لقد كان تطور الذكاء الاصطناعي دائمًا هو الحال في DeepSeek Math V2 حيث أن التحقق الذاتي هو جوهر التفكير العميق، وليس فقط النماذج أو البيانات الأكبر.

جربه اليوم وأخبرني بأفكارك في قسم التعليقات أدناه!